9급 지방직 공무원 수학(2016. 6. 18.) 시험일자 : 2016년 6월 18일
1. 실수a,b에 대하여 42a=3, 42b=7 일 때, a+b의 값은?
- ① log2110
- ② log2142
- ③ log4210
- ④ log4221
등록된 댓글이 없습니다.
2. 두 집합 X,Y에 대하여 연산 △를 X△Y=(X-Y)∪(Y-X)로 정의할 때, 세 집합 a{2,3,4,5}, B={2,3,5,7}, C={3,5,7}에 대하여 집합 (A△B)△C의 모든 원소의 합은?
- ① 6
- ② 9
- ③ 12
- ④ 13
등록된 댓글이 없습니다.
3. 무리함수 에 대하여 다음 중 옳은 것은?
- ① 정의역은 {x|x≤-2}이다.
- ② 치역은 {y|y≥-1}이다.
- ③ 그래프는 점 (2,3)을 지난다.
- ④ 그래프는 제4사분면을 지난다.
등록된 댓글이 없습니다.
4. 을 간단히 하면? (단, b<a<0)
- ① -2a
- ② -2b
- ③ 2a
- ④ 2b
등록된 댓글이 없습니다.
5. 0≤x≤6에서 정의된 함수 y=f(x)의 그래프가 그림과 같을 때, 다음 중 옳은 것은?
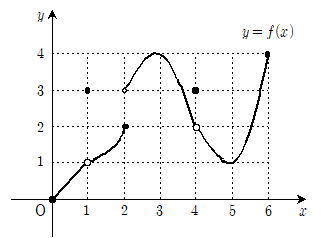
- ① f(2)=f(4)
- ② 는 존재한다.
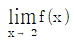
- ③ 는 존재하지 않는다.
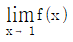
- ④ 0<x<6에서 f(x)가 불연속인 점이 3개 있다.
등록된 댓글이 없습니다.
6. 이차함수 f(x)가 모든 실수 x에 대하여 f(4+x)=f(4-x)를 만족시키고 f(4)=3, f(3)=5일 때, f(1)의 값은?
- ① 19
- ② 21
- ③ 23
- ④ 25
등록된 댓글이 없습니다.
7. 최고차항의 계수가 1인 이차함수 f(x)가 를 만족시킬 때, f(2)의 값은?
- ① 9
- ② 12
- ③ 15
- ④ 18
등록된 댓글이 없습니다.
8. 점 A(-2,-1)에서 원x2+y2-8x-y+15=0 위를 움직이는 점 P까지의 거리의 최댓값을 M, 최솟값을 m이라고 할 때, M과 의 곱Mm의 값은?
- ① 40
- ② 42
- ③ 44
- ④ 46
등록된 댓글이 없습니다.
9. 다항식 f(x)를 x2-4로 나눈 나머지가 x+3일 때, (x-2)f(x)를 x+2로 나눈 나머지는?
- ① -4
- ② -3
- ③ -2
- ④ -1
등록된 댓글이 없습니다.
10. 수열 {an}, {bn에 대하여 다음 중 항상 참인 명제는?
- ① 이고 이면 이다.

- ② 이고 이면 이다.
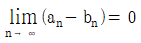
- ③ 모든 자연수 n에 대하여 an<bn이면 이다.
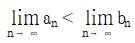
- ④ 모든 자연수 n에 대하여 an<bn이고 이면 이다.
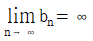
등록된 댓글이 없습니다.
11. 의 값은?
- ① 1/2
- ② 1
- ③ 3/2
- ④ 2
등록된 댓글이 없습니다.
12. n이 10 이하의 자연수일 때, 이 실수가 되도록 하는 n의 개수는? (단, i=√-1)
- ① 0
- ② 2
- ③ 3
- ④ 5
등록된 댓글이 없습니다.
13. 5개의 문자 D, R, E, A, M을 일렬로 나열할 때, A와 M이 이웃하는 경우의 수는?
- ① 16
- ② 24
- ③ 48
- ④ 60
등록된 댓글이 없습니다.
14. 이차방정식 2x2+x-2=0의 두 근을 α, β라고 할 때, α2β-αβ2의 값은? (단, α>β)
- ①

- ②

- ③
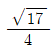
- ④
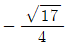
등록된 댓글이 없습니다.
15. 함수 f(x)=x3+3x2-x+6의 그래프 위의 점 (t, f(t))에서의 접선의 기울기를 g(t)라고 할 때, g(t)의 최솟값은?
- ① -4
- ② -1
- ③ 3
- ④ 6
등록된 댓글이 없습니다.
16. 두 집합 A={a, 3a}, B={b, b2}에 대하여 A=B일 때, a/b의 값은? (단, 0<b<1)
- ① 3
- ② 1/3
- ③ 1/9
- ④ 1/27
등록된 댓글이 없습니다.
17. 모든 실수 에 대하여 이차부등식 -x2+2ax≤2a가 성립하도록 하는 정수a 의 개수는?
- ① 0
- ② 1
- ③ 2
- ④ 3
등록된 댓글이 없습니다.
18. 을 만족시키는 상수 a,b의 합 a+b의 값은?
- ① -3
- ② -2
- ③ -1
- ④ 0
등록된 댓글이 없습니다.
19. 의 값은?
- ① 2009
- ② 2016
- ③ 2023
- ④ 2030
등록된 댓글이 없습니다.
20. 두 사건 A, B가 서로 배반사건이고 P(A)=1/6, P(A|BC)=1/4일 때, P(B|AC)의 값은? (단, P(BC)≠0)
- ① 1/5
- ② 2/5
- ③ 3/5
- ④ 4/5
등록된 댓글이 없습니다.