9급 지방직 공무원 수학(2015. 6. 27.) 시험일자 : 2015년 6월 27일
1. 두 함수 f, g에 대하여 f(x)=3x+2, (gㆍf)x2+1일 때, g(11)의 값은?
- ① 10
- ② 11
- ③ 12
- ④ 13
등록된 댓글이 없습니다.
2. 함수 f(x)=x3+x+1에 대하여 의 값은?
- ① 2
- ② 4
- ③ 6
- ④ 8
등록된 댓글이 없습니다.
3. 행렬 의 역행렬 A-1의 모든 성분의 합은?
- ① 1
- ② 2
- ③ 3
- ④ 4
등록된 댓글이 없습니다.
4. 지수함수 y=3a-x+b의 그래프가 점 (-1, 4)를 지나고, 그래프의 점근선이 y=1일 때, 두 상수 a, b의 합 a+b의 값은?
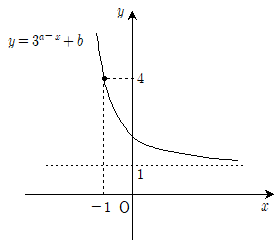
- ① 1
- ② 2
- ③ 3
- ④ 4
등록된 댓글이 없습니다.
5. 부등식 x + y + z ≤ 2를 만족하는 음이 아닌 정수 x, y, z의 순서쌍 (x, y, z)의 개수는?
- ① 7
- ② 10
- ③ 13
- ④ 16
등록된 댓글이 없습니다.
6. 이차함수 f(x)가 모든 실수 x에 대하여 f(x)=f(6-x)를 만족시키고 이차항의 계수가 양수일 때, f(x)의 최솟값은?
- ① f(0)
- ② f(1)
- ③ f(2)
- ④ f(3)
등록된 댓글이 없습니다.
7. 한 개의 동전을 64번 던질 때, 앞면이 28번 이상 36번 이하로 나올 확률을 표준정규분포표를 이용하여 구한 것은?

- ① 0.5328
- ② 0.6826
- ③ 0.7745
- ④ 0.8664
등록된 댓글이 없습니다.
8. 원 x2+y2=25와 직선 y=x+4가 만나는 두 점을 A, B라 할 때, 선분 AB의 길이는?
- ① 2√11
- ② 2√13
- ③ 2√15
- ④ 2√17
등록된 댓글이 없습니다.
9. 집합 X는 공집합이 아니고, 정수를 원소로 가진다. X를 정의역으로 하는 두 함수 f, g가 f(x)=x3+1, g(x)=3x-1일 때, f=g가 되는 집합 X의 개수는?
- ① 1
- ② 2
- ③ 3
- ④ 4
등록된 댓글이 없습니다.
10. 사차함수 f(x)와 그 도함수 f′(x)가 다음 조건을 만족시킬 때, f(3)/f(2)의 값은?

- ① 64/9
- ② 81/16
- ③ 1/4
- ④ 121/36
등록된 댓글이 없습니다.
11. 두 수열 {an}, {bn}에 대하여 일 때, 의 값은?
- ① 1
- ② 2
- ③ 3
- ④ 4
등록된 댓글이 없습니다.
12. 다항식 x3+ax2+bx+1을 x+1과 x-1로 나눈 나머지가 각각 -2, 2일 때, 두 상수 a, b의 곱 ab의 값은?
- ① -2
- ② -1
- ③ 1
- ④ 2
등록된 댓글이 없습니다.
13. 다항함수 f(x)에 대하여 일 때, f(1)의 값은?
- ① 8
- ② 10
- ③ 12
- ④ 16
등록된 댓글이 없습니다.
14. 로그방정식 (log3x)2 - 5log3x+4=0의 두 근의 합은?
- ① 72
- ② 76
- ③ 80
- ④ 84
등록된 댓글이 없습니다.
15. 직선 3x-4x+12=0이 x축의 양의 방향과 이루는 각의 크기를 θ라 할 때, 의 값은?
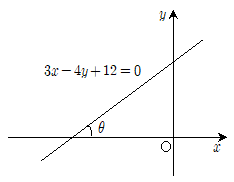
- ① 1/5
- ② 2/5
- ③ 3/5
- ④ 4/5
등록된 댓글이 없습니다.
16. 명제 'x ≥ 6이면 2x + a ≤ 3x - 2a이다.’가 참이 되기 위한 실수 a의 범위는?
- ① a ≤ 2
- ② a ≥ 2
- ③ a ≤ 3
- ④ a ≥ 3
등록된 댓글이 없습니다.
17. 함수 y=x2-5x+4의 그래프 위의 점 P(a, b)에 대하여 a의 범위가 0 ≤ a ≤ 4일 때, a+b의 최댓값은?
- ① 3
- ② 4
- ③ 5
- ④ 6
등록된 댓글이 없습니다.
18. 두 점 A(3, 0)과 B(1, 2)에 대하여 원점 O를 지나는 직선 ℓ이 선분 AB와 만나는 점을 P라 하자. 삼각형 OAP의 넓이가 1일 때 직선 ℓ의 기울기는?
- ① 1/7
- ② 2/7
- ③ 3/7
- ④ 4/7
등록된 댓글이 없습니다.
19. 수열 {an}이 an+1=-1n3n-1을 만족시킬 때, 의 값은?
- ① 600
- ② 620
- ③ 640
- ④ 660
등록된 댓글이 없습니다.
20. 그림과 같이 이차함수 y=f(x)는 최솟값 α를 갖고 f(α)=f(β)=0이다. 방정식 (fㆍf)(x)=0의 서로 다른 실근의 개수는?
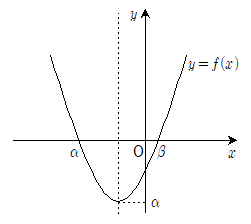
- ① 1
- ② 2
- ③ 3
- ④ 4
등록된 댓글이 없습니다.