9급 지방직 공무원 수학(2015. 3. 14.) 시험일자 : 2015년 3월 14일
1. 전체집합 U의 임의의 두 부분집합 A, B에 대하여 다음 중 항상 옳은 것은? (단, U는 유한집합이고, 임의의 집합 S에 대하여 n(S)는 S원소의 개수를, SC는 S의 여집합을 나타낸다)
- ① n(A∪B)=n(A)+n(B)
- ② n(A∪BC)=n(U)-n(B)
- ③ n(A-B)=n(A)-n(B)
- ④ n(AC∩BC)=n(U)-n(A∪B)
등록된 댓글이 없습니다.
2. 다음 <보기>에 대한 설명으로 옳은 것은?
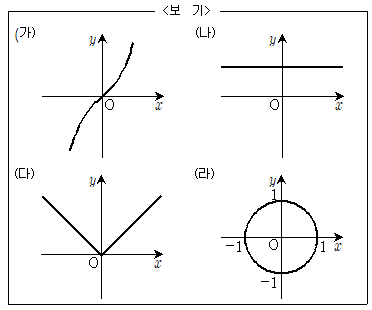
- ① 함수의 그래프는 4개이다.
- ② (나)는 항등함수이다.
- ③ (다)는 상수함수이다.
- ④ 일대일함수의 그래프는 1개이다.
등록된 댓글이 없습니다.
3. 좌표평면상에서 그림과 같이 중심이 원점 O인 임의의 원을 10등분하여 각 분점을 차례로 P0, P1…, P9이라 하자. ∠P0OP1=θ라 할 때, sinθ+sin(2θ)+…+sin(10θ)의 값은?

- ① 0
- ② π
- ③ 2π
- ④ 3π
등록된 댓글이 없습니다.
4. x+y=2√5, xy=4, x>y일 때, x/y-y/x의 값은?
- ① √2
- ② √3
- ③ 2
- ④ √5
등록된 댓글이 없습니다.
5. 임의의 두 실수 a, b에 대하여 연산 *을 a*b=a+b+4라고 정의할 때, 연산 *에 대한 2의 역원은?
- ① -10
- ② -4
- ③ 4
- ④ 10
등록된 댓글이 없습니다.
6. 두 실수 x, y에 대하여 복소수 z-xy+(x+y)i가 , 을 만족할 때, x2+y2의 값은? (단, i=√-1이고 는 z의 켤레복소수이다.)
- ① 1
- ② 3
- ③ 5
- ④ 7
등록된 댓글이 없습니다.
7. 좌표평면 위의 점 P가 원점 O 및 x축 위의 한 점 A(5, 0)에 대하여 를 유지하며 움직인다. 이때, 점 P가 그리는 도형의 길이는?
- ① 12π
- ② 14π
- ③ 16π
- ④ 18π
등록된 댓글이 없습니다.
8. ∠B=π/3, 인 삼각형 ABC의 넓이는?
- ① 2√3
- ② 6
- ③ 12
- ④ 8√3
등록된 댓글이 없습니다.
9. 함수 의 역함수가 일 때, 상수 a, b, c의 합 a+b+c의 값은?
- ① -2
- ② -1
- ③ 1
- ④ 2
등록된 댓글이 없습니다.
10. 삼각형 ABC의 세 변 AB, BC, CA의 길이를 각각 c, a, b라 하자. 세 변의 길이 a, b, c가 관계식 2b2=a2+c2을 만족할 때, 각 B의 최댓값은?
- ① π/6
- ② π/4
- ③ π/3
- ④ π/2
등록된 댓글이 없습니다.
11. 상수 a, b에 대하여 행렬 가 을 만족할 때, a-b의 값은?
- ① 2
- ② 3
- ③ 4
- ④ 5
등록된 댓글이 없습니다.
12. 두 함수 y=3, y=3x/9 의 그래프와 직선 y=3의 교점을 각각 P, Q라 할 때, 선분 PQ의 길이는?
- ① 1
- ② 2
- ③ 3
- ④ 4
등록된 댓글이 없습니다.
13. 수열 {an}에 대하여 a1=2이고 an+1=2an-1일 때, a10의 값은?
- ① 512
- ② 513
- ③ 1024
- ④ 1025
등록된 댓글이 없습니다.
14. 방사선 입자가 보호막을 한 개 통과할 때마다 방사선 입자의 양은 직전의 2/5가 된다고 하자. 이때, 방사선 입자의 양이 처음의 1/100이하가 되도록 하기 위해 필요한 최소한의 보호막의 개수는? (단, log2=0.310으로 계산한다)
- ① 6개
- ② 7개
- ③ 8개
- ④ 9개
등록된 댓글이 없습니다.
15. 양수 a, b에 대하여 라 할 때, 의 값은?
- ① 8
- ② 9
- ③ 10
- ④ 11
등록된 댓글이 없습니다.
16. 다음 <보기> 중 x=1에서 연속인 함수만을 모두 고른 것은?

- ① ㄱ, ㄷ
- ② ㄴ, ㄹ
- ③ ㄷ, ㄹ
- ④ ㄱ, ㄴ, ㄹ
등록된 댓글이 없습니다.
17. 미분 가능한 함수 f(x)에 대하여 다음의 함수 g(x)가 모든 실수 x에 대하여 연속일 때, f′(1)의 값은?
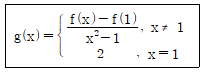
- ① 1
- ② 2
- ③ 3
- ④ 4
등록된 댓글이 없습니다.
18. 구간 [0, d]에서 정의된 함수 y==f(x)의 그래프가 다음과 같을 때, 함수 의 최댓값은? (단, 상수 a, b, c, d는 0 < a < b <c < d를 만족한다.)

- ① g(a)
- ② g(b)
- ③ g(c)
- ④ g(d)
등록된 댓글이 없습니다.
19. 연속확률변수 X의 확률밀도함수가 일 때, 확률 의 값은? (단, a는 양의 상수이다)
- ① 9/16
- ② 21/32
- ③ 3/4
- ④ 27/32
등록된 댓글이 없습니다.
20. 영업팀 직원 2명, 재무팀 직원 3명, 인사팀 직원 4명으로 구성된 동호회 회원들을 일렬로 세울 때, 인사팀 직원끼리 서로 이웃하지 않을 확률은?
- ① 5/9
- ② 5/42
- ③ 5/36
- ④ 5/18
등록된 댓글이 없습니다.