9급 지방직 공무원 서울시 수학(지적)(2016. 6. 25.) 시험일자 : 2016년 6월 25일
1. 공간 R3의 점 A(1. 0, -1), B(2, 1, -1), C(1, 2, 1)에 대해 ∠BAC는?
- ① π/4
- ② π/3
- ③ π/2
- ④ 2π/3
등록된 댓글이 없습니다.
2. -1 ≤ x ≤ 3 인 범위에서 이차함수 y=x2-4x+2 의 최솟값과 최댓값의 차이는?
- ① 6
- ② 7
- ③ 8
- ④ 9
등록된 댓글이 없습니다.
3. 이차함수 f(x)=x2-4x+a 의 그래프를 y축의 방향으로 -5만큼 평행이동시킨 그래프가 x축에 접할 때, 상수 a의 값은?
- ① 6
- ② 7
- ③ 8
- ④ 9
등록된 댓글이 없습니다.
4. x, y에 대한 연립방정식 에서 x=0, y=0 이외의 해를 갖게 하는 실수 a의 값을 모두 구했을 때, 이들의 합은?
- ① -1
- ② -2
- ③ -3
- ④ -4
등록된 댓글이 없습니다.
5. 방정식 4x-9⋅2x+20=0 의 두 실근을 α, β라 할 때, 2α+β의 값은?
- ① 18
- ② 19
- ③ 20
- ④ 21
등록된 댓글이 없습니다.
6. x에 관한 10차 다항식 을 x-1 로 나눈 나머지는 7이고, x+1 로 나눈 나머지는 3이다. 홀수차 항의 계수의 합인 a1+a3+a5+a7+a9 의 값은?
- ① 1
- ② 2
- ③ 3
- ④ 4
등록된 댓글이 없습니다.
7. 좌표평면에서 점(x, y)가 부등식 2x2 ≤ y ≤ x+1 의 영역을 움직일 때, x+y 의 최댓값과 최솟값의 합은?
- ① 17/8
- ② 19/8
- ③ 21/8
- ④ 23/8
등록된 댓글이 없습니다.
8. 세 수 A=√35, B=105/6, C=11/(4-√5) 의 대소 관계로 옳은 것은?
- ① A < B < C
- ② A < C < B
- ③ C < A < B
- ④ C < B < A
등록된 댓글이 없습니다.
9. 의 값은?
- ① (1/3)√2
- ② (2/3)√2
- ③ √2
- ④ (4/3)√2
등록된 댓글이 없습니다.
10. 곡선 과 x축 및 직선 x=2 에 둘러싸인 도형을 y축의 둘레로 회전시킬 때 생기는 회전체의 부피는?
- ① (29/15)π
- ② (31/15)π
- ③ (32/15)π
- ④ (34/15)π
등록된 댓글이 없습니다.
11. 다음과 같이 정의된 수열 {an}이 있다. 이때, 의 값은?
- ① 250
- ② 300
- ③ 500
- ④ 1000
등록된 댓글이 없습니다.
12. 원 x2+y2=4 와 직선 x+y=1 의 두 교점을 A와 B라 할 때, 점 A와 점 B사이의 거리는? (단, x와 y는 실수이다.)
- ① √14
- ② 4
- ③ 3√2
- ④ 2√5
등록된 댓글이 없습니다.
13. 수열 {an}에 대하여 an이 일 때, 의 값은?
- ① 1
- ② 3/2
- ③ 2
- ④ 5/2
등록된 댓글이 없습니다.
14. 1<a<10 인 자연수 a와 자연수 m이 다음 식 (a-1)⋅10m<3⋅2100<a⋅10m 을 만족할 때, a+m의 값은? (단, log102=0.3010, log103=0.4771 로 계산한다.)
- ① 30
- ② 32
- ③ 34
- ④ 36
등록된 댓글이 없습니다.
15. 삼차함수 f(x)=5x3+3x2+ax+b 에 대하여 두 등식 가 성립할 때, 실수 a와 b의 합 a+b 의 값은?
- ① -2
- ② -1
- ③ 0
- ④ 1
등록된 댓글이 없습니다.
16. 다항함수 f(x)가 모든 실수 x에 대하여 등식 f(x)=x3+f'(1)x2+x를 만족시킬 때, f(-1)의 값은?
- ① -3
- ② -4
- ③ -5
- ④ -6
등록된 댓글이 없습니다.
17. 이고 6sin2θ=5cosθ 가 성립할 때, sinθ, cosθ, tanθ의 대소 관계로 옳은 것은?
- ① sinθ<cosθ<tanθ
- ② sinθ<tanθ<cosθ
- ③ tanθ<sinθ<cosθ
- ④ tanθ<cosθ<sinθ
등록된 댓글이 없습니다.
18. 를 만족시키는 실수인 두 상수 a와 b의 곱 ab의 값은?
- ① -1/2
- ② -2/3
- ③ 1/2
- ④ 2/3
등록된 댓글이 없습니다.
19. 구간 [ -1, 1]에서 정의된 확률변수 X의 확률밀도함수 f(x)가 f(x)=(1/2)x2+a 일 때, P(0≤X≤3a)의 값은? (단, a는 상수이다.)
- ① 1/2
- ② 1/3
- ③ 1/4
- ④ 1/5
등록된 댓글이 없습니다.
20. 어느 자격시험에 응시한 사람들의 점수는 평균 620점, 표준편차 50점인 정규분포를 따르고, 이 시험에 합격하기 위해서는 660점 이상의 점수를 얻어야 한다고 한다. 이 시험에 응시한 사람이 660점 이상의 점수를 받을 확률은? (단, 아래 표준정규분포표를 이용한다.)
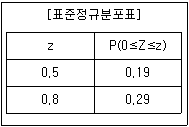
- ① 0.21
- ② 0.31
- ③ 0.48
- ④ 0.58
등록된 댓글이 없습니다.