9급 국가직 공무원 통계학개론(2022. 4. 2.) 시험일자 : 2022년 4월 2일
1. 두 지역 A, B의 소득에 대한 상자 그림(box plot)은 다음과 같다. 이에 대한 설명으로 옳은 것만을 모두 고르면?

- ① ㄱ, ㄴ
- ② ㄱ, ㄷ
- ③ ㄴ, ㄷ
- ④ ㄱ, ㄴ, ㄷ
등록된 댓글이 없습니다.
2. 다음 제시된 두 변수 X와 Y에 대한 산점도 중 X와 Y의 표본상관계수(피어슨의 표본상관계수)가 가장 큰 것은?
- ①
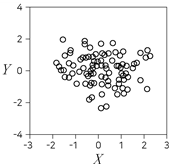
- ②
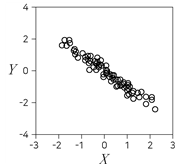
- ③
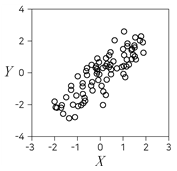
- ④
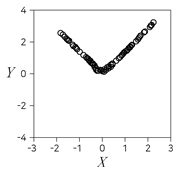
등록된 댓글이 없습니다.
3. 통계적 가설검정에서 제1종 오류확률에 대한 설명으로 옳은 것은?
- ① 귀무가설이 참일 때 귀무가설을 기각할 확률
- ② 귀무가설이 참일 때 귀무가설을 기각하지 않을 확률
- ③ 귀무가설이 거짓일 때 귀무가설을 기각할 확률
- ④ 귀무가설이 거짓일 때 귀무가설을 기각하지 않을 확률
등록된 댓글이 없습니다.
4. 단순선형회귀모형 Yi = β0 + β1x1 + εi, (i = 1, 2, …, 22) 에서 최소제곱법으로 회귀식을 추정한 후 잔차제곱합을 구하였더니 2,100이었다. 이때 오차항 분산(σ2)의 불편추정값은? (단, εi는 N(0, σ2)를 따르고 서로 독립이다)
- ① 100
- ② 105
- ③ 110
- ④ 120
등록된 댓글이 없습니다.
5. 코로나바이러스 감염 상황과 진단키트의 진단 확률이 다음과 같을 때, 한 사람의 진단키트 결과가 음성이라면 이 사람이 실제 음성일 확률은?

- ① 13/15
- ② 9/10
- ③ 14/15
- ④ 29/30
등록된 댓글이 없습니다.
6. 두 연속형 확률변수 X와 Y가 독립일 때, 이에 대한 설명으로 옳지 않은 것은?
- ① X와 Y의 공분산은 0이다.
- ② X와 Y의 합에 대한 분산은 X와 Y의 분산의 합이다.
- ③ X와 Y의 곱에 대한 기댓값은 X와 Y의 기댓값의 곱이다.
- ④ X가 주어졌을 때 Y의 조건부확률밀도함수는 X의 주변확률밀도함수와 같다.
등록된 댓글이 없습니다.
7. 다음은 단순선형회귀모형을 적합하여 얻은 분산분석표이다. 이에 대한 설명으로 옳지 않은 것은?
- ① (가)의 값은 540이다.
- ② (나)의 값은 20이다.
- ③ (다)의 값은 27이다.
- ④ 모형의 결정계수는 200/740 이다.
등록된 댓글이 없습니다.
8. 다음은 시장조사에서 세탁기 색에 대한 선호도를 알아보기 위해 최근 판매된 세탁기의 색을 조사한 결과이다. 선호하는 색이 4:4:1:1의 비율로 분포한다는 가설을 검정하려 할 때, 이에 대한 설명으로 옳은 것만을 모두 고르면?

- ① ㄱ, ㄴ
- ② ㄱ, ㄷ
- ③ ㄴ, ㄷ
- ④ ㄱ, ㄴ, ㄷ
등록된 댓글이 없습니다.
9. 분포에 대한 설명으로 옳지 않은 것은?
- ① 확률변수 F가 자유도(df1, df2)인 F분포를 따를 때, 1/F은 자유도(df2, df1)인 F분포를 따른다.
- ② 평균이 μ이고 분산이 σ2인 정규모집단에서 임의로 추출한 n개의 확률변수에 대한 표본평균 는 를 따른다.
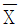
- ③ 확률변수 X1, X2, …, Xn이 서로 독립이며 표준정규분포를 따르면 X12 + X22 + … + Xn2은 자유도가 n인 카이제곱분포를 따른다.
- ④ 평균이 μ이고 분산이 σ2인 모집단에서 임의로 추출한 5개의 확률변수에 대한 표본평균이 일 때, 는 근사적으로 표준정규분포를 따른다.
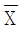
등록된 댓글이 없습니다.
10. 세 가지 필터의 성능을 비교하기 위해 일원배치 분산분석법(one-way analysis of variance)을 실시하여 얻은 분산분석표의 일부가 다음과 같을 때 (가)의 값은?
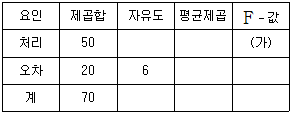
- ① 2.5
- ② 5.0
- ③ 7.5
- ④ 15.0
등록된 댓글이 없습니다.
11. 다음은 어느 확률변수의 확률밀도함수이다. 이에 대한 설명으로 옳은 것만을 모두 고르면? (단, 함수는 0을 기준으로 좌우 대칭이다)
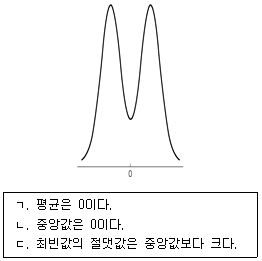
- ① ㄱ
- ② ㄱ, ㄴ
- ③ ㄴ, ㄷ
- ④ ㄱ, ㄴ, ㄷ
등록된 댓글이 없습니다.
12. 어느 지역에서 20대 남자의 몸무게는 평균이 μ이고 표준편차가 8인 정규분포를 따른다고 한다. 이 지역에서 임의추출한 20대 남자 64명의 평균 몸무게가 66일 때, 모평균 μ에 대한 95% 신뢰구간은? (단, 단위는 kg이며, 표준정규분포를 따르는 확률변수 Z에 대하여 P(Z≥1.96) = 0.025, P(Z≥1.645) = 0.05 이다)
- ① (64.040, 67.960)
- ② (64.355, 67.645)
- ③ (65.755, 66.245)
- ④ (65.794, 66.206)
등록된 댓글이 없습니다.
13. 다중선형회귀모형 Yi = β0 + β1xi1 + β2xi2 + εi, (i = 1, 2, …,n) 에서 최소제곱법으로 구한 분산분석표의 F-값에 대한 p-값(유의확률)이 0.05보다 작다. 유의수준 5%에서 내릴 수 있는 결론으로 옳은 것은? (단, εi는 N(0, σ2)를 따르고 서로 독립이다)
- ① β1≠0 이고 β2≠0
- ② β1≠0 또는 β2≠0
- ③ β0≠0 이고 β1≠0 이고 β2≠0
- ④ β0≠0 또는 β1≠0 또는 β2≠0
등록된 댓글이 없습니다.
14. 확률변수 X에 대하여 Var(3X+9) = 36, E(X(X+1)) = 10 을 만족할 때, E(X)의 값은? (단, E(X) > 0 이다)
- ① 1
- ② 2
- ③ 3
- ④ 4
등록된 댓글이 없습니다.
15. 독립인 두 모집단 1과 2에 대한 확률분포는 각각 다음과 같다. 모집단 i에서 임의로 추출한 100개의 확률변수의 평균을 라 할 때, 의 근사분포는?
- ①

- ②
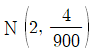
- ③
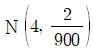
- ④
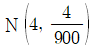
등록된 댓글이 없습니다.
16. 모평균과 모분산이 알려지지 않고 서로 독립인 두 개의 정규모집단에서 각각 25개씩 표본을 임의추출한 후, 두 모집단의 모분산을 비교할 때 사용하는 분포는?
- ① 표준정규분포
- ② 자유도가 24인 t분포
- ③ 자유도가 24인 카이제곱분포
- ④ 자유도가 (24, 24)인 F분포
등록된 댓글이 없습니다.
17. 성별과 와인 생산지의 선호도가 관련이 있는지를 알아보기 위해 100명을 임의추출한 후 성별과 와인 생산지 선호도를 조사하여 작성한 분할표가 다음과 같다. 성별과 와인 생산지 선호도가 관련이 있는지를 검정하는 카이제곱검정통계량의 값은?
- ①
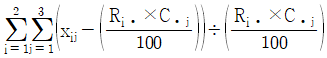
- ②
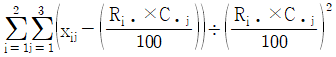
- ③
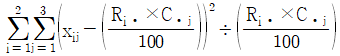
- ④
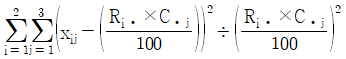
등록된 댓글이 없습니다.
18. 다음은 서로 독립인 두 지역 A와 B에서 실시하는 복지 프로그램 수혜자의 평균연령을 비교하기 위하여 두 지역의 복지 프로그램 수혜자 중에서 A지역에서 100명, B지역에서 200명을 임의추출하여 연령을 조사한 결과이다. A지역에서 복지 혜택을 받는 사람의 평균 연령을 μA라고 하고, B지역에서 복지 혜택을 받는 사람의 평균 연령을 μB라고 할 때, 가설 H0 : μA = μB 대 H1 : μA ≠ μB를 검정하기 위한 p-값(유의확률)은? (단, Z는 표준정규분포를 따르는 확률변수이다)
- ①
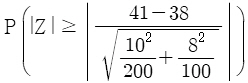
- ②
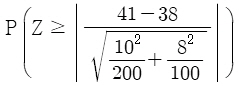
- ③
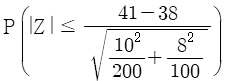
- ④
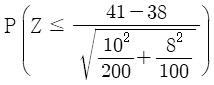
등록된 댓글이 없습니다.
19. 다음은 두 인자 A와 B에 대하여 이원배치법을 적용한 실험 결과의 분산분석표 일부이다. 실험에서 인자의 수준조합에 대한 반복실험수는 동일하다. 이에 대한 설명으로 옳지 않은 것은?

- ① (가)는 3이고 (나)는 4이다.
- ② 분석에 사용한 자료의 수는 모두 15개이다.
- ③ 인자 A와 인자 B의 수준의 수는 각각 2와 4이다.
- ④ 인자 A에 대한 주효과는 유의수준 5%에서 유의하다.
등록된 댓글이 없습니다.
20. 정규분포로부터 임의추출한 자료의 정규확률그림(정규분포 분위수대분위수 그림, normal probability plot)은?
- ①
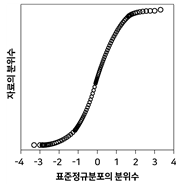
- ②
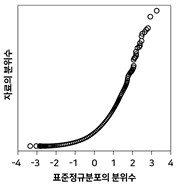
- ③
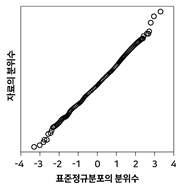
- ④
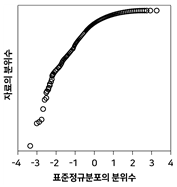
등록된 댓글이 없습니다.