경찰공무원(순경) 수학(2019. 4. 27.) 시험일자 : 2019년 4월 27일
1. 최고차항의 계수가 1인 삼차다항식 f(x)를 x-1로 나누었을 때 나머지는 3이고, x-3으로 나누었을 때도 나머지가 3이다. f(x)가 x-2로 나누어떨어질 때, f(4)의 값은?
- ① 15
- ② 16
- ③ 17
- ④ 18
등록된 댓글이 없습니다.
2. 방정식 x3 - 1 = 0의 한 허근을 ω라 할 때, (2- ω19)(2 - ω-19의 값은? (단, 는 ω의 켤레복소수이다.)
- ① 3
- ② 5
- ③ 7
- ④ 9
등록된 댓글이 없습니다.
3. x2 - xy + ax – 2y2 - 8y – 8이 x, y에 대한 일차식의 곱으로 인수분해될 때, 상수 a의 값은?
- ① -3
- ② -2
- ③ -1
- ④ 0
등록된 댓글이 없습니다.
4. 양의 실수 a, b에 대하여 직선 이 점 을 지날 때, ab의 최솟값은?
- ① 10
- ② 12
- ③ 14
- ④ 16
등록된 댓글이 없습니다.
5. 임의의 실수 a에 대하여 점 A(-1, 1)과 직선 y = ax + 2a + 3 사이의 거리의 최댓값은?
- ① √5
- ② √7
- ③ 2√3
- ④ 3√2
등록된 댓글이 없습니다.
6. 최고차항의 계수가 1인 이차함수 y = f(x)가 점 A(1, 3)을 지나고, 꼭짓점은 제3사분면에 있으면서 직선 y = -x-2 위에 있다. 이때, 이차함수 y = f(x)의 최솟값은?
- ① -7
- ② -5
- ③ -3
- ④ -1
등록된 댓글이 없습니다.
7. 좌표평면에서 원 (x-1)2 + (y-1)2 = 1을 y축에 대하여 대칭이동한 후 y축의 방향으로 1만큼 평행이동한 원 위의 임의의 점과 원점 사이의 거리의 최댓값을 a, 최솟값을 b라 할 때, a+b의 값은?
- ① √5
- ② 2√5
- ③ 3√5
- ④ 4√5
등록된 댓글이 없습니다.
8. 함수 y = g(x)의 그래프는 유리함수 의 그래프를 x축의 방향으로 –2만큼, y축의 방향으로 3만큼 평행이동한 그래프이다. 함수 y = g(x)의 그래프에서 두 점근선의 교점이 y = f(x)의 그래프 위의 점일 때, 상수 k의 값은?
- ① 7/2
- ② 5/4
- ③ 7/4
- ④ 6/5
등록된 댓글이 없습니다.
9. 이차방정식 x2 + x – 1 = 0의 두 근을 α, β라 할 때, 의 값은?
- ① 215
- ② 220
- ③ 230
- ④ 235
등록된 댓글이 없습니다.
10. 수열 {an}에 대하여 이 수렴할 때, 의 값은?
- ①

- ②
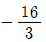
- ③

- ④
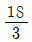
등록된 댓글이 없습니다.
11. log3(-n3 + 15n2 - 66n + 80)의 값이 존재하도록 하는 모든 자연수 n의 값의 합은?
- ① 8
- ② 10
- ③ 12
- ④ 14
등록된 댓글이 없습니다.
12. 이차방정식 x2 - 4x + 2 = 0의 두 근을 α, β라 할 때, 의 값은? (단, α<β)
- ① 1
- ② √2
- ③ 2
- ④ 2√2
등록된 댓글이 없습니다.
13. 함수 에 대하여 두 함수 g(x), h(x)가 g(x) = (f(x))2, h(x) = (x-1)f(x) 일 때, 함수 g(x)의 불연속인 점의 개수를 a, 함수 h(x)의 불연속인 점의 개수를 b라 하자. 이때 a+b의 값은?
- ① 0
- ② 1
- ③ 2
- ④ 3
등록된 댓글이 없습니다.
14. 점 A(1, -2)에서 곡선 y = x2 + x에 그은 접선은 2개 있다. 그 2개의 접선의 방정식을 각각 y = f1(x), y = f2(x)라 할 때, f1(2) + f2(2)의 값은?
- ① 2
- ② 4
- ③ 6
- ④ 8
등록된 댓글이 없습니다.
15. -√2 < a < √2인 실수 a에 대하여, 함수 f(x) = (x2-2)(x-a)는 극댓값 f(α)와 극솟값 f(β)를 갖는다. 일 때, f(3αβ)의 값은?
- ① 2
- ② -2
- ③ -6
- ④ -10
등록된 댓글이 없습니다.
16. 의 값은?
- ① 0
- ② 1/4
- ③ 1/2
- ④ 3/4
등록된 댓글이 없습니다.
17. 다항함수 f(x)가 , f(1) = -4를 만족시킬 때, 함수 f(x)의 최솟값은?
- ①
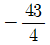
- ②
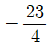
- ③
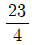
- ④
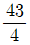
등록된 댓글이 없습니다.
18. 다항함수 f(x)가 를 만족시킬 때, f′(2)의 값은?
- ① -32
- ② -16
- ③ -4
- ④ -1
등록된 댓글이 없습니다.
19. 검은 상자에 1부터 20까지의 자연수가 각각 하나씩 적힌 20개의 공이 들어 있다. 이 상자에서 임의로 2개의 공을 동시에 꺼내 공에 적힌 수를 확인하고 공을 다시 상자에 넣는 시행을 한다. 이 시행을 2번 했을 때, 20이 적힌 공이 나올 확률은?
- ① 11/100
- ② 3/20
- ③ 19/100
- ④ 23/100
등록된 댓글이 없습니다.
20. A지역 경찰공무원의 1년 평균 휴가일을 확률변수 X라 하면 X는 정규분포 N(m, 3.62)을 따른다고 한다. A지역 경찰공무원 중에서 임의로 추출한 36명의 1년 평균 휴가일의 표본평균을 라 하자. 일 때, m의 값은? (단, 아래의 표준정규분포표를 이용하여 구하시오.)
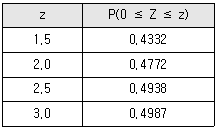
- ① 12
- ② 15
- ③ 17.5
- ④ 18.5
등록된 댓글이 없습니다.