경찰공무원(순경) 수학(2018. 9. 1.) 시험일자 : 2018년 9월 1일
1. x = 3 + √3, y = 3 - √3일 때, 의 값은?
- ① 4
- ② 6
- ③ 3√3
- ④ 4√3
등록된 댓글이 없습니다.
2. x3 - 1 = 0의 한 허근을 ω라 할 때, ω + ω3 + ω5 + … + ω2017 + ω2019을 간단히 하면?
- ① 0
- ② ω
- ③ ω+1
- ④ 1
등록된 댓글이 없습니다.
3. x100을 x(x-1)(x+1)로 나눈 나머지는?
- ① x2
- ② x2 - 1
- ③ x2 + 1
- ④ x2 - x
등록된 댓글이 없습니다.
4. a>0, b>0일 때, 의 최솟값은?
- ① 1
- ② 2
- ③ 1/2
- ④ 5/2
등록된 댓글이 없습니다.
5. x에 대한 이차부등식 f(x)<0의 해가 2<x<5가 될 때, 부등식 을 만족시키는 정수 x의 개수를 구하면?
- ① 5
- ② 6
- ③ 7
- ④ 8
등록된 댓글이 없습니다.
6. 이차함수 y = x2 + ax + a의 그래프와 직선 y = 2x + 2가 한 점에서 접할 때, 실수 a의 값을 합하면?
- ① 4
- ② 6
- ③ 8
- ④ 10
등록된 댓글이 없습니다.
7. 두 함수 f(x) = log3x, g(x) = 3x에서 의 값은?
- ① 1/3
- ② 1
- ③ 3
- ④ 4
등록된 댓글이 없습니다.
8. 원 x2 + y2 = 9와 직선 y = √3x + 3이 서로 다른 두 점 P, Q에서 만날 때, 선분 PQ의 길이는?
- ① 3√3
- ②
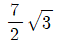
- ③ 4√3
- ④
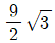
등록된 댓글이 없습니다.
9. log2 = 0.3010, log3 = 0.4771일 때, 1212은 몇 자리의 정수인가?
- ① 12
- ② 13
- ③ 14
- ④ 15
등록된 댓글이 없습니다.
10. 의 값은?
- ①
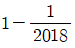
- ②

- ③

- ④
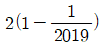
등록된 댓글이 없습니다.
11. 다항함수 f(x)에 대하여 일 때, f(2)의 값은?
- ① 2
- ② 4
- ③ 6
- ④ 8
등록된 댓글이 없습니다.
12. 함수 f(x)가 양의 실수 x에 대하여 2x2-1<f(x)<2x2+x+1을 만족할 때, 의 값은?
- ① 1
- ② 2
- ③ 3
- ④ 4
등록된 댓글이 없습니다.
13. x≥-1인 임의의 실수 x에서 연속인 함수 f(x)가 , f(3) = 2를 만족시킬 때, 두 상수 a, b의 합 a+b의 값은?
- ① 2
- ② 4
- ③ 6
- ④ 8
등록된 댓글이 없습니다.
14. 수열 {an}에 대하여 일 때, 의 값은?
- ① -2
- ② -1
- ③ 0
- ④ 6
등록된 댓글이 없습니다.
15. 공차가 양수인 두 등차수열 {an}, {bn}이 있다. 수열 {an}, {bn}의 첫째항부터 제 n항까지의 합을 각각 Sn, Tn이라고 할 때, 이다. 의 값은?
- ①
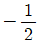
- ②
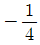
- ③
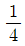
- ④
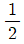
등록된 댓글이 없습니다.
16. 함수 에 대하여 의 값은?
- ① 50
- ② 55
- ③ 60
- ④ 65
등록된 댓글이 없습니다.
17. 연속함수 f(x)가 (단, a는 상수)일 때, 의 값은?
- ① 7/6
- ② 5/6
- ③ 1/2
- ④ 1/6
등록된 댓글이 없습니다.
18. 방정식 x2 + 2y + 4z = 6를 만족시키는 음이 아닌 정수해의 순서쌍 (x, y, z)의 개수는?
- ① 1
- ② 2
- ③ 3
- ④ 4
등록된 댓글이 없습니다.
19. 닫힌구간 [2, 3]에서 정의된 연속확률변수 X에 대하여 라 할 때, 평균 E(X)의 값은? (단, 2 ≤ t ≤ 3 이고 a는 상수이다.)
- ①
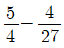
- ②
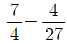
- ③
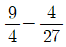
- ④
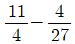
등록된 댓글이 없습니다.
20. 어떤 약의 질병 A에 대한 치료율이 0.9라고 한다. 이 약을 질병 A환자 1000명에게 투여했을 때, 치료되는 환자의 수가 919명 이상일 확률은? (단, 치료 유무는 약 투여에 의해서만 결정되고 3√10 = 9.5라고 하자.)
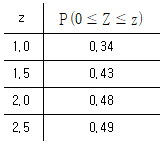
- ① 0.16
- ② 0.07
- ③ 0.02
- ④ 0.01
등록된 댓글이 없습니다.