9급 지방직 공무원 응용역학개론(2019. 6. 15.) 시험일자 : 2019년 6월 15일
1. 그림과 같이 x-y평면 상에 있는 단면 중 도심의 y좌표 값이 가장 작은 것은?
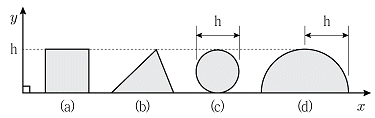
- ① (a)
- ② (b)
- ③ (c)
- ④ (d)
등록된 댓글이 없습니다.
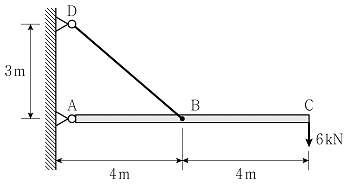
2. 그림과 같이 강체로 된 보가 케이블로 B점에서 지지되고 있다. C점에 수직하중이 작용할 때, 부재 AB에 발생되는 축력의 크기[kN]는? (단, 모든 부재의 자중은 무시한다)
- ① 12 (압축)
- ② 12 (인장)
- ③ 16 (압축)
- ④ 16 (인장)
등록된 댓글이 없습니다.
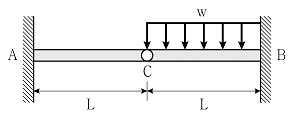
3. 그림과 같이 C점에 내부힌지가 있는 보의 지점 A와 B에서 수직반력의 비 RA/RB는? (단, 보의 휨강성 EI는 일정하고, 자중은 무시한다)
- ① 3/13
- ② 3/14
- ③ 3/15
- ④ 3/16
등록된 댓글이 없습니다.
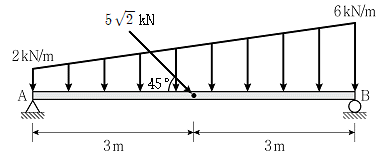
4. 그림과 같은 분포하중과 집중하중을 받는 단순보에서 지점 A의 수직반력 크기[kN]는? (단, 보의 휨강성 EI는 일정하고, 자중은 무시한다)
- ① 10.0
- ② 12.5
- ③ 15.0
- ④ 17.5
등록된 댓글이 없습니다.
5. 그림과 같은 부정정보에서 지점 B에 발생하는 수직반력 RB의 크기[kN]는? (단, 보의 휨강성 EI는 일정하며, 자중은 무시한다)

- ① 55
- ② 60
- ③ 65
- ④ 70
등록된 댓글이 없습니다.
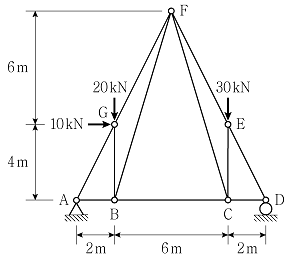
6. 그림과 같은 트러스 구조물에서 부재 BC의 부재력 크기[kN]는? (단, 모든 자중은 무시한다)
- ① 7 (인장)
- ② 7 (압축)
- ③ 5 (인장)
- ④ 5 (압축)
등록된 댓글이 없습니다.
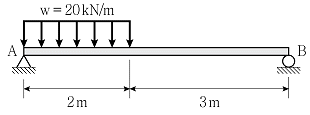
7. 그림과 같은 등분포하중이 작용하는 단순보에서 최대휨모멘트가 발생되는 거릿값(x)과 최대휨모멘트 값(M)의 비는? (단, 보의 휨강성 EI는 일정하고, 자중은 무시하며, 최대휨모멘트의 발생지점은 지점 A로부터의 거리이다)
- ① 1/8
- ② 8
- ③ 1/16
- ④ 16
등록된 댓글이 없습니다.
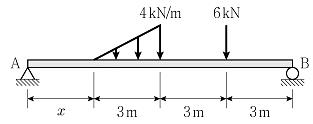
8. 그림과 같은 단순보에 하중이 작용할 때 지점 A, B에서 수직 반력 RA 및 RB가 2RA=RB로 성립되기 위한 거리 [m]는? (단, 보의 휨강성 EI는 일정하고, 자중은 무시한다)
- ① 3
- ② 4
- ③ 5
- ④ 6
등록된 댓글이 없습니다.
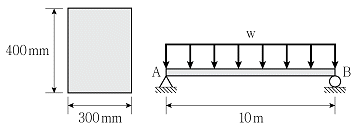
9. 그림과 같이 폭 300mm, 높이 400mm의 직사각형 단면을 갖는 단순보의 허용 휨응력이 6MPa이라면, 단순보에 작용시킬 수 있는 최대 등분포하중 w의 크기[kN/m]는? (단, 보의 휨강성 EI는 일정하고, 자중은 무시한다)
- ① 6.84
- ② 5.84
- ③ 4.84
- ④ 3.84
등록된 댓글이 없습니다.
10. 그림과 같이 내부힌지가 있는 보에서, 지점 B의 휨모멘트와 CD구간의 최대휨모멘트가 같게 되는 길이 a는? (단, 보의 휨강성 EI는 일정하고, 자중은 무시한다)

- ①
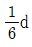
- ②
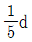
- ③
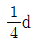
- ④

등록된 댓글이 없습니다.
11. 그림과 같은 음영 부분 A단면에서 x-x축으로부터 도심까지의 거리 y는?

- ① 5D/12
- ② 6D/12
- ③ 7D/12
- ④ 8D/12
등록된 댓글이 없습니다.
12. 그림과 같이 재료와 길이가 동일하고 단면적이 다른 수직 부재가 축하중 P를 받고 있을 때, A점에서 발생하는 변위는 B점에서 발생하는 변위의 몇 배인가? (단, 구간 AB와 BC의 축강성은 각각 EA와 2EA이고, 부재의 자중은 무시한다)
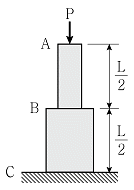
- ① 1.5
- ② 2.0
- ③ 2.5
- ④ 3.0
등록된 댓글이 없습니다.
13. 그림과 같은 삼각형 단면의 축에 대한 단면2차모멘트 Ix[mm4]는?
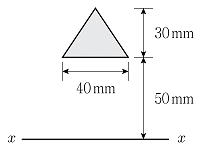
- ① 526×104
- ② 345×104
- ③ 219×104
- ④ 155×104
등록된 댓글이 없습니다.
14. 그림과 같이 캔틸레버보에 집중하중(P), 등분포하중(w), 모멘트하중(M)이 작용하고 있다. 자유단 A에 최대 수직처짐을 발생시키는 하중은 이 세 가지 중 어느 것이며, 보에 세 하중이 동시에 작용할 때 발생하는 수직처짐 의 크기[mm]는? (단, P=10kN, w=10kN/m, M=10kNㆍm, 휨강성 EI=2×1010kNㆍmm2이고, 자중은 무시한다)
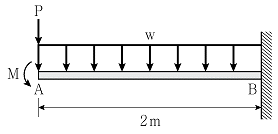
- ① w =10kN/m, δ =1mm
- ② M =10kNㆍm, δ =1mm
- ③ P =10kN, δ =10/3mm
- ④ M =10kNㆍm, δ =10/3mm
등록된 댓글이 없습니다.
15. 그림과 같은 단순보에서 집중하중이 작용할 때, O점에서의 수직 처짐 δo의 크기[mm]는? (단, 휨강성 EI=2×1012Nㆍmm2이며, 자중은 무시한다)
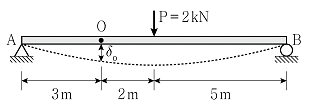
- ① 14.5
- ② 15.5
- ③ 16.5
- ④ 17.5
등록된 댓글이 없습니다.
16. 그림과 같은 하중을 받는 트러스에 대한 설명으로 옳지 않은 것은? (단, 모든 부재의 자중은 무시한다)
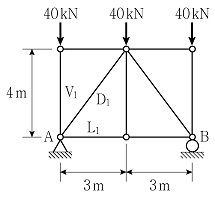
- ① D1은 16kN의 압축을 받는다.
- ② 내적안정이고 외적안정이면서 정정이다.
- ③ L1은 15kN의 인장을 받는다.
- ④ V1은 40kN의 압축을 받는다.
등록된 댓글이 없습니다.
17. 그림과 같이 두 개의 재료로 이루어진 합성 단면이 있다. 단면 하단으로부터 중립축까지의 거리 C[mm]는? (단, 각각 재료의 탄성계수는 E1=0.8×105MPa, E2=3.2×105MPa이다)
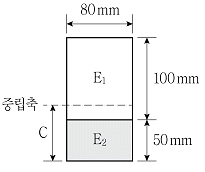
- ① 50
- ② 60
- ③ 70
- ④ 80
등록된 댓글이 없습니다.
18. 그림과 같은 부재에 2개의 축하중이 작용할 때 구간 D1, D2, D3의 변위의 비(δ1:δ2:δ3)는? (단, 모든 부재의 단면적은 A로 나타내며, 탄성계수 E는 일정하고, 자중은 무시한다)
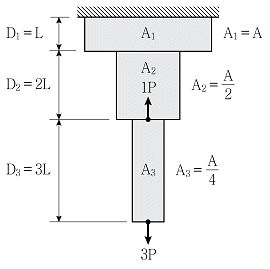
- ① 1:2:18
- ② 1:4:18
- ③ 1:2:24
- ④ 1:4:24
등록된 댓글이 없습니다.
19. 그림과 같이 양단이 고정지지된 직사각형 단면을 갖는 기둥의 최소 임계하중의 크기[kN]는? (단, 기둥의 탄성계수 E=210GPa, π2은 10으로 계산하며, 자중은 무시한다)
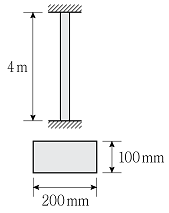
- ① 9,750
- ② 9,250
- ③ 9,000
- ④ 8,750
등록된 댓글이 없습니다.
20. 그림과 같은 변단면 캔틸레버보에서 A점의 수직처짐의 크기는? (단, 모든 부재의 탄성계수 E는 일정하고, 자중은 무시한다)
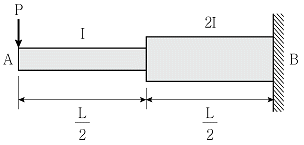
- ①

- ②

- ③
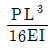
- ④
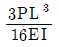
등록된 댓글이 없습니다.