9급 지방직 공무원 서울시 전기이론(2019. 6. 15.) 시험일자 : 2019년 6월 15일
1. 그림의 회로에서 i1+i2+i3의 값[A]은?

- ① 40[A]
- ② 41[A]
- ③ 42[A]
- ④ 43[A]
등록된 댓글이 없습니다.
2. 그림과 같이 한 접합점에 전류가 유입 또는 유출된다. 일 때, 전류 i4의 값[A]은?

- ① 10sint[A]
- ② 10√2sint[A]
- ③

- ④

등록된 댓글이 없습니다.
3. 그림의 회로에서 v(t=0)=V0일 때, 시간 t에서의 v(t)의 값[V]은?

- ① v(t)=V0e-10t[V]
- ② v(t)=V0e0.1t[V]
- ③ v(t)=V0e10t[V]
- ④ v(t)=V0e-0.1t[V]
등록된 댓글이 없습니다.
4. 그림의 회로에서 C=200[pF]의 콘덴서가 연결되어 있을 때, 시정수 τ[psec]와 단자 a-b 왼쪽의 테브냉 등가전압 VTh의 값[V]은?

- ① τ=1200[psec], VTh=24[V]
- ② τ=1200[psec], VTh=12[V]
- ③ τ=600[psec], VTh=12[V]
- ④ τ=600[psec], VTh=24[V]
등록된 댓글이 없습니다.
5. 그림과 같은 전압 파형이 100[mH] 인덕터에 인가되었다. t=0[sec]에서 인덕터 초기 전류가 0[A]라고 한다면, t=14[sec]일 때 인덕터 전류의 값[A]은?

- ① 210[A]
- ② 220[A]
- ③ 230[A]
- ④ 240[A]
등록된 댓글이 없습니다.
6. 20[Ω]의 저항에 실효치 20[V]의 사인파가 걸릴 때 발생열은 직류 전압 10[V]가 걸릴 때 발생열의 몇 배인가?
- ① 1배
- ② 2배
- ③ 4배
- ④ 8배
등록된 댓글이 없습니다.
7. 교류전원 vs(t)=2cos2t[V]가 직렬 RL회로에 연결되어 있다. R=2[Ω], L=1[H]일 때, 회로에 흐르는 전류 i(t)의 값[A]은?

- ①

- ②
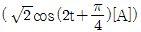
- ③

- ④

등록된 댓글이 없습니다.
8. 단면적은 A, 길이는 L인 어떤 도선의 저항의 크기가 10[Ω]이다. 이 도선의 저항을 원래 저항의 1/2로 줄일 수 있는 방법으로 가장 옳지 않은 것은?
- ① 도선의 길이만 기존의 1/2로 줄인다.
- ② 도선의 단면적만 기존의 2배로 증가시킨다.
- ③ 도선의 도전율만 기존의 2배로 증가시킨다.
- ④ 도선의 저항률만 기존의 2배로 증가시킨다.
등록된 댓글이 없습니다.
9. 그림의 회로에서 1[Ω]에서의 소비전력이 4[W]라고 할 때, 이 회로의 전압원의 전압 Vs[V]의 값과 2[Ω] 저항에 흐르는 전류 I2의 값[A]은?

- ① Vs=5[V], I2=2[A]
- ② Vs=5[V], I2=3[A]
- ③ Vs=6[V], I2=2[A]
- ④ Vs=6[V], I2=3[A]
등록된 댓글이 없습니다.
10. 정전용량이 C0[F]인 평행평판 공기 콘덴서가 있다. 이 극판에 평행하게, 판 간격 d[m]의 4/5 두께가 되는 비유전율 εs인 에보나이트 판으로 채우면, 이때의 정전 용량의 값[F]은?

- ①

- ②

- ③

- ④

등록된 댓글이 없습니다.
11. 그림의 회로에서 전류 i의 값[A]은?

- ① 3/4[A]
- ② 5/4[A]
- ③ 7/4[A]
- ④ 9/4[A]
등록된 댓글이 없습니다.
12. 그림과 같이 전압원 Vs는 직류 1[V], R1=1[Ω], R2=1[Ω], R3=1[Ω], L1=1[H], L2=1[H]이며, t=0일 때, 스위치는 단자 1에서 단자 2로 이동했다. t=∞일 때, i1의 값[A]은?

- ① 0[A]
- ② 0.5[A]
- ③ -0.5[A]
- ④ -1[A]
등록된 댓글이 없습니다.
13. 그림과 같은 회로에서 단자 A, B 사이의 등가저항의 값[kΩ]은?

- ① 0.5[kΩ]
- ② 1.0[kΩ]
- ③ 1.5[kΩ]
- ④ 2.0[kΩ]
등록된 댓글이 없습니다.
14. 그림에서 ㈎의 회로를 ㈏와 같은 등가회로로 구성한다고 할 때, x+y의 값은?

- ① 3
- ② 4
- ③ 5
- ④ 6
등록된 댓글이 없습니다.
15. 그림과 같은 자기회로에서 철심의 자기저항 Rc의 값[Aㆍ turns/Wb]은? (단, 자성체의 비투자율 μr1은 100이고, 공극 내 비투자율 μr2은 1이다. 자성체와 공극의 단면적은 4[m2]이고, 공극을 포함한 자로의 전체길이 Lc=52[m]이며, 공극의 길이 Lg=2[m]이다. 누설 자속은 무시한다.)

- ① 1/32π×107[A ㆍ turns/Wb]
- ② 1/16π×107[A ㆍ turns/Wb]
- ③ 1/8π×107[A ㆍ turns/Wb]
- ④ 1/4π×107[A ㆍ turns/Wb]
등록된 댓글이 없습니다.
16. 그림과 같은 전압 파형의 실횻값[V]은? (단, 해당 파형의 주기는 16[sec]이다.)

- ① √3[V]
- ② 2[V]
- ③ √5[V]
- ④ √6[V]
등록된 댓글이 없습니다.
17. 시변 전계, 시변 자계와 관련한 Maxwell 방정식의 4가지 수식으로 가장 옳지 않은 것은?
- ①

- ②

- ③

- ④

등록된 댓글이 없습니다.
18. 무한히 먼 곳에서부터 A점까지 +3[C]의 전하를 이동 시키는 데 60[J]의 에너지가 소비되었다. 또한 무한히 먼 곳에서부터 B점까지 +2[C]의 전하를 이동시키는 데 10[J]의 에너지가 생성되었다. A점을 기준으로 측정한 B점의 전압[V]은?
- ① -20[V]
- ② -25[V]
- ③ +20[V]
- ④ +25[V]
등록된 댓글이 없습니다.
19. 그림과 같은 연산증폭기 회로에서 v1=1[V], v2=2[V], R1=1[Ω], R2=4[Ω], R3=1[Ω], R4=4[Ω]일 때, 출력 전압 v0의 값[V]은? (단, 연산증폭기는 이상적이라고 가정한다.)

- ① 1[V]
- ② 2[V]
- ③ 3[V]
- ④ 4[V]
등록된 댓글이 없습니다.
20. 커패시터 양단에 인가되는 전압이 v(t)=5sin(120πt-π/3)[V]일 때, 커패시터에 입력되는 전류는 i(t)=0.03πcos(120πt-π/3)[A]이다. 이 커패시터의 커패시턴스의 값[μF]은?
- ① 40[μF]
- ② 45[μF]
- ③ 50[μF]
- ④ 55[μF]
등록된 댓글이 없습니다.