9급 지방직 공무원 수학(2017. 4. 8.) 시험일자 : 2017년 4월 8일
1. 일 때, a+b의 값은? (단, a, b는 실수)
- ① -2
- ② -1
- ③ 0
- ④ 1
등록된 댓글이 없습니다.
2. 다항식 x5+x4을 x2-4로 나누었을 때의 나머지는?
- ① 16-x32
- ② 16x-16
- ③ 16x+16
- ④ 16x+32
등록된 댓글이 없습니다.
3. 두 집합 X={x|-1≤x≤4}, Y={y|-5≤y≤5}에 대하여 함수 f:X→Y가 (f(x)=ax+b(a<0)이다. 이 함수 f가 일대일 대응이 되도록 하는 두 상수 a, b에 대하여 a+b의 값은?
- ① 1
- ② 2
- ③ 3
- ④ 4
등록된 댓글이 없습니다.
4. 다음 함수의 그래프 중에서 x축의 방향 또는 y축의 방향으로 평행이동하여 서로 겹칠 수 없는 것은?
- ①
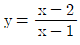
- ②
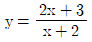
- ③

- ④
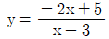
등록된 댓글이 없습니다.
5. x2+x+1=0, y4-y2+1=01일 때, x6-y6의 값은?
- ① 0
- ② 1
- ③ 2
- ④ 3
등록된 댓글이 없습니다.
6. 이차함수 y=x2-3x의 그래프와 직선 y=x+k가 적어도 한 점에서 만나도록 하는 실수 k의 값의 범위는?
- ① k≤-8
- ② -8≤k≤-6
- ③ -6≤k≤-4
- ④ k≤-4
등록된 댓글이 없습니다.
7. x>0일 때, 함수 의 최솟값은?
- ① -6
- ② -7
- ③ -8
- ④ -9
등록된 댓글이 없습니다.
8. 직선 3x-4y+1=0을 x축에 대하여 대칭이동한 직선이 원 (x-k)2+(y-2)2=16의 넓이를 이등분할 때, 상수 k의 값은?
- ① -2
- ② -3
- ③ -4
- ④ -5
등록된 댓글이 없습니다.
9. 함수 에 대하여 의 값은?
- ① 4
- ② 9/2
- ③ 5
- ④ 11/2
등록된 댓글이 없습니다.
10. 다항함수 f(x)에 대하여 이 성립할 때, f(3)f′(3)의 값은?
- ① 15
- ② 20
- ③ 25
- ④ 30
등록된 댓글이 없습니다.
11. 전체집합 U의 두 부분집합 A, B에 대하여 A⊂B일 때, 다음 중 항상 성립하는 것은? (단, Ac은 A의 여집합)
- ① Ac∪B=ø
- ② A∩Bc=U
- ③ A∩B=B
- ④ Bc⊃Ac
등록된 댓글이 없습니다.
12. 부정적분 를 구하면?
- ① (단, C는 적분상수)
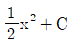
- ② x2+C(단, C는 적분상수)
- ③ 2x2+C(단, C는 적분상수)
- ④ (단, C는 적분상수)
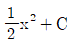
등록된 댓글이 없습니다.
13. 세 수 a, b, c가 이 순서대로 등차수열을 이루고, 세 수 -b, 4,8a 가 이 순서대로 등비수열을 이룰 때, a+b의 값은? (단, b는 자연수)
- ① 1
- ② 2
- ③ 3
- ④ 4
등록된 댓글이 없습니다.
14. log35를 log35=n+α(n은 정수, 0≤α<1)로 표현할 때, 9α의 값은?
- ① 5/3
- ② 25/9
- ③

- ④
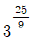
등록된 댓글이 없습니다.
15. 의 전개식에서 1/x2의 계수가 240일 때, 실수 a의 값은?
- ① 2
- ② 3
- ③ 4
- ④ 5
등록된 댓글이 없습니다.
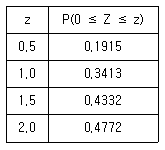
16. 확률변수 X가 정규분포 (N120, 62)을 따를 때, 주어진 표준정규분포표를 이용하여 확률 P(117≤X≤132)를 구하면?
- ① 0.5328
- ② 0.6247
- ③ 0.6687
- ④ 0.4445
등록된 댓글이 없습니다.
17. 이고 일 때, a+b의 값은?
- ① 5/2
- ② 3
- ③ 7/2
- ④ 4
등록된 댓글이 없습니다.
18. 부등식 x2+y2-2x2y≤0을 만족하는 실수 x, y에 대하여 x+y의 최댓값은?
- ① √2
- ② 2
- ③ 2√25
- ④ 4
등록된 댓글이 없습니다.
19. 미분가능한 함수 f(x)가 을 만족시키고 f′(0)=12일 때, f(0)의 값은?
- ① -8
- ② -6
- ③ -4
- ④ -2
등록된 댓글이 없습니다.
20. 함수 f(x)의 도함수 f′(x)가 f′(x)=6x2-8이고 f(0)=0일 때, 곡선 y=f(x)와 x축으로 둘러싸인 도형의 넓이는?
- ① 12
- ② 16
- ③ 20
- ④ 24
등록된 댓글이 없습니다.