9급 지방직 공무원 응용역학개론(2017. 6. 17.) 시험일자 : 2017년 6월 17일
1. 그림과 같이 보 BD가 같은 탄성계수를 갖는 케이블 AB와 CD에 의해 수직하중 P를 지지하고 있다. 케이블 AB의 길이가 L이라 할 때, 보 BD가 수평을 유지하기 위한 케이블 CD의 길이는? (단, 보 BD는 강체이고, 케이블 AB의 단면적은 케이블 CD의 단면적의 3배이며, 모든 자중은 무시한다)
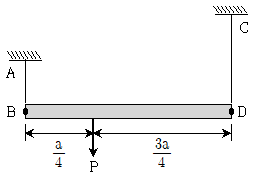
- ① 1/L
- ② 3L/4
- ③ L
- ④ 3L
등록된 댓글이 없습니다.
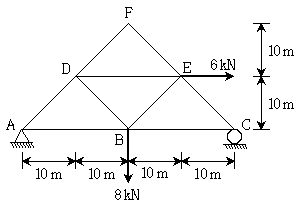
2. 그림과 같은 트러스 구조물에서 부재 AD의 부재력[kN]은? (단, 모든 자중은 무시한다)
- ①
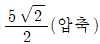
- ②

- ③

- ④
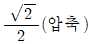
등록된 댓글이 없습니다.
3. 지름 d=50mm, 길이 L=1m인 강봉의 원형단면 도심에 축방향 인장력이 작용했을 때 길이는 1mm 늘어나고, 지름은 0.0055mm 줄어들었다. 탄성계수 E=1.998×105[N/mm2]라면 전단탄성계수 G의 크기[N/mm2]는? (단, 강봉의 축강성은 일정하고, 자중은 무시한다)
- ① 9.0×104
- ② 10.0×104
- ③ 12.0×104
- ④ 15.0×104
등록된 댓글이 없습니다.
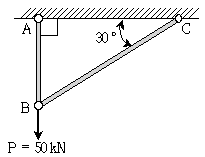
4. 그림과 같이 50kN의 수직하중이 작용하는 트러스 구조물에서 BC 부재력의 크기[kN]는? (단, 모든 자중은 무시한다)
- ① 0
- ② 25
- ③ 50
- ④ 100
등록된 댓글이 없습니다.
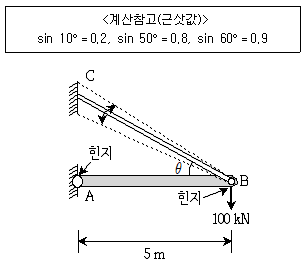
5. 케이블 BC의 허용축력이 150kN일 때, 그림과 같은 100kN의 수직하중을 지지할 수 있는 구조물에서, 경사각 0°≤θ≤60°일 때, 가장 작은 단면의 케이블을 사용하려고 한다. 필요한 경사각의 크기는? (단, 봉 AB는 강체로 가정하고, 모든 자중과 미소변형 및 케이블의 처짐은 무시한다)
- ① 10°
- ② 30°
- ③ 50°
- ④ 60°
등록된 댓글이 없습니다.
6. 그림과 같은 정정보의 휨변형에 의한 B점의 수직 변위의 크기[mm]는? (단, B점은 힌지이고, 휨강성 EI=100,000kNㆍm2이고, 자중은 무시한다)

- ① 3.6
- ② 7.2
- ③ 12.2
- ④ 14.4
등록된 댓글이 없습니다.
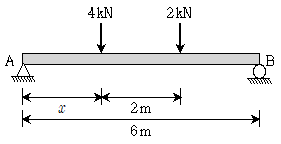
7. 그림과 같은 단순보의 수직 반력 RA 및 RB가 같기 위한 거리 x의 크기[m]는? (단, 보의 휨강성 EI는 일정하고, 자중은 무시한다)
- ① 7/3
- ② 8/3
- ③ 10/3
- ④ 11/3
등록된 댓글이 없습니다.
8. 그림과 같이 길이가 L인 부정정보에서, B지점이 δ만큼 침하하였다. 이때 B지점에 발생하는 반력의 크기는? (단, 보의 휨강성 EI는 일정하고, 자중은 무시하며, 휨에 의한 변형만을 고려한다)

- ①
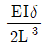
- ②
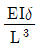
- ③
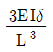
- ④

등록된 댓글이 없습니다.
9. 그림과 같은 외팔보의 자유단에 모멘트 하중(=PㆍL)이 작용할 때 보에 저장되는 탄성 변형에너지와 동일한 크기의 탄성 변형에너지를 집중하중을 이용하여 발생시키고자 할 때, 보의 자유단에 작용시켜야 하는 수직하중 Q의 크기는? (단, 모든 보의 휨강성 EI는 일정하고, 자중은 무시한다)
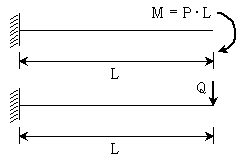
- ① √2P
- ② 2√2P
- ③ √3P
- ④ 2√3P
등록된 댓글이 없습니다.
10. 그림의 봉 부재는 단면적이 10,000mm2이며, 단면도심에 압축하중 P를 받고 있다. 이 부재의 변형에너지밀도(strain energy density, u)가 u=0.01N/mm2일 때, 수평하중 P의 크기[kN]는? (단, 부재의 축강성 EA=500kN이고, 자중은 무시한다)
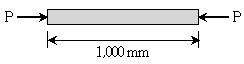
- ① 10
- ② 11
- ③ 100
- ④ 110
등록된 댓글이 없습니다.
11. 그림과 같이 x-y평면상에 있는 단면의 최대 주단면 2차모멘트 Imax[mm4]는? (단, 축과 축의 원점 C는 단면의 도심이다. 단면 2차모멘트는 Ix=3mm4, Iy=7mm4이며, 최소 주단면 2차모멘트 Imin=2mm4이다)
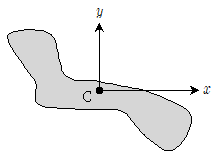
- ① 5
- ② 6
- ③ 7
- ④ 8
등록된 댓글이 없습니다.
12. 그림과 같이 2개의 힘이 동일점 O에 작용할 때, 두 힘 U, V의 합력의 크기[kN]는?
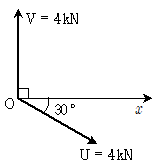
- ① 1
- ② 2
- ③ 3
- ④ 4
등록된 댓글이 없습니다.
13. 공칭응력(nominal stress)과 진응력(true stress, 실제응력), 공칭변형률(nominal strain)과 진변형률(true strain, 실제변형률)에 대한 설명으로 옳은 것은?
- ① 변형이 일어난 단면에서의 실제 단면적을 사용하여 계산한 응력을 공칭응력이라고 한다.
- ② 모든 공학적 용도에서는 진응력과 진변형률을 사용하여야 한다.
- ③ 인장실험의 경우 진응력은 공칭응력보다 크다.
- ④ 인장실험의 경우 진변형률은 공칭변형률보다 크다.
등록된 댓글이 없습니다.
14. 그림과 같은 하중을 받는 사각형 단면의 탄성 거동하는 짧은 기둥이 있다. A점의 응력이 압축이 되기 위한 P1/P2의 최솟값은? (단, 기둥의 자중은 무시한다)
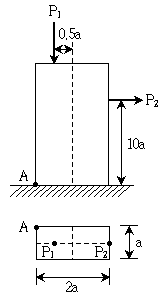
- ① 6
- ② 8
- ③ 10
- ④ 12
등록된 댓글이 없습니다.
15. 그림과 같은 라멘 구조물에서 지점 A의 반력의 크기[kN]는? (단, 모든 부재의 축강성과 휨강성은 일정하고, 자중은 무시한다)
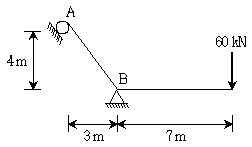
- ① 60
- ② 84
- ③ 105
- ④ 140
등록된 댓글이 없습니다.
16. 그림과 같은 삼각형 단면에서 y축에서 도심까지의 거리는?
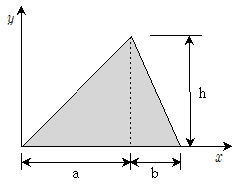
- ① 2a+b/3
- ② a+2b/4
- ③ a+b/3
- ④ a+2b/3
등록된 댓글이 없습니다.
17. 그림과 같은 양단 고정보에 수직하중이 작용할 때, 하중 작용점 위치의 휨모멘트 크기[kNㆍm]는? (단, 보의 휨강성 EI는 일정하고, 자중은 무시한다)

- ① 125
- ② 250
- ③ 275
- ④ 400
등록된 댓글이 없습니다.
18. 그림과 같이 트러스 부재들의 연결점 B에 수직하중 P가 작용하고 있다. 모든 부재들의 길이 L, 단면적 A, 탄성계수 E가 같은 경우, 부재 BC의 부재력은? (단, 모든 자중은 무시한다)
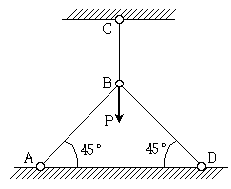
- ① P/3(압축)
- ② P/2(인장)
- ③ 2P/3(압축)
- ④ 3P/4(인장)
등록된 댓글이 없습니다.
19. 그림과 같은 구조물에서 C점에 단위크기(=1)의 수직방향 처짐을 발생시키고자 할 때, C점에 가해 주어야 하는 수직하중 P의 크기는? (단, 모든 자중은 무시하고, AC, BC 부재의 단면적은 A, 탄성계수는 E인 트러스 부재이다)
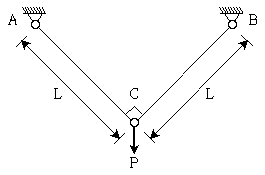
- ① EA/4L
- ② EA/3L
- ③ EA/2L
- ④ EA/L
등록된 댓글이 없습니다.
20. 단면적 500mm2, 길이 1m인 강봉 단면의 도심에 100kN의 인장력을 주었더니, 길이가 1mm 늘어났다. 이 강봉의 탄성계수 E[N/mm2]는? (단, 강봉의 축강성은 일정하고, 자중은 무시한다)
- ① 1.0×105
- ② 1.5×105
- ③ 1.8×105
- ④ 2.0×105
등록된 댓글이 없습니다.